General form of a linear equation
ax + by + c = 0.
Two linear equations in the same two variables are called a pair of linear equations in two variables.
The general form of the equations
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
where a1, a2, b1, b2, c1 and c2 are real numbers
Points to remember
- The graph of a linear equation is a straight line.
- A pair of values of variables ‘x‘ and ‘y’ which satisfy both the equations in the given system of equations is said to be a solution of the pair of linear equations.
Representation of a pair of linear equations in two variables:
(i) Graphical method
(ii) Algebraic method
Methods to solve a pair of linear equations using ALGEBRAIC METHOD-
- Substitution Method
- Elimination Method
- Cross Multiplication Method
GRAPHICAL METHOD (Graphical Representation)
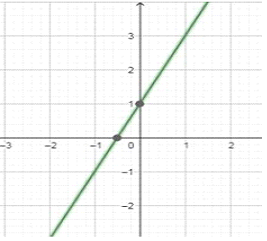
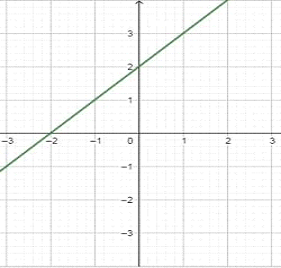
Example: Draw the graph of y=2x+1
Types of Lines
A pair of linear equations in two variables can be represented as:-
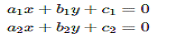
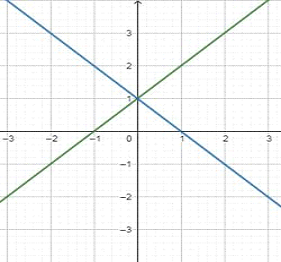
- INTERSECTING LINES
They intersect at exactly one point.
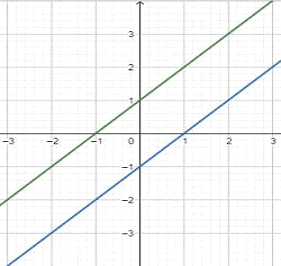
PARALLEL LINES
They never intersect each other.
COINCIDENT LINES
They Coincide each other.
Consistency of System
A system of two linear equations can have one solution, an infinite number of solutions, or no solution.
If a system has at least one solution, it is said to be consistent .
If a system has no solution, it is said to be inconsistent.
If a consistent system has exactly one solution, it is independent .
If a consistent system has an infinite number of solutions, it is dependent .
| Relationship between coefficients |
Graph | Number of Solutions | Consistency of System |
| a1/a2≠b1/b2 | Intersecting lines | Unique solution | Consistent |
| a1/a2=b1/b2≠c1/c2 | Parallel lines | No solution | Inconsistent |
| a1/a2=b1/b2=c1/c2 | Co-incident lines | Infinite solutions | Consistent |
- SUBSTITUTION METHOD
In this method, the value of one variable from one equation is substituted in the other equation.
Example: Solve the following system by substitution.
2x – 3y = –2———>1
4x + y = 24———>2
4x + y = 24
y = –4x + 24——>3
Now substitute the value of y in equation (1) and solve for x:
2x – 3(–4x + 24) = –2
2x + 12x – 72 = –2
14x = 70
x = 5
Now put x=5 in equation (3)
y = –4(5) + 24 = –20 + 24 = 4
So, the solution is (x, y) = (5, 4).
- ELIMINATION METHOD
The elimination method is used to solve linear equations in two variables, where one of the variables is removed or eliminated.
Example:
2x + 7y = 10…………….. (1)
3x + y = 6………………… (2)
First way,
Multiply equation (1) by 3 and equation (2) by 2, we get,
6x + 21y = 30……………..(3)
6x + 2y = 12……………….(4)
The coefficients the x in equation (3) and equation (4) are the same i.e. 6.
Now, subtract equation (4) from equation (3). We get-
6x + 21y – 6x – 2y = 30 – 12
⇒ 19y = 18
y = 18/19
Substitute the value of y in either equation (1) or (2),
Lets put it in equation (2).
3x + 18/19 = 6
3x = 6 – 18/19
3x = 96/19
x = 96/57 = 32/19
Second way,
Multiply equation (2) with 7,
21x + 7y = 42………….(5)
And equation (1) is 2x + 7y = 10
Subtracting equation (1) from equation (5), we get
19x = 32
x = 32/19
Substituting the value of x in Eqn. (1),
2(32/19) + 7y = 10
7y = 10 – 64/19
7y = 126/19
y = 18/19
- CROSS MULTIPLICATION METHOD
This is the simplest method and gives the accurate value of the variables.
Example: Solve the following linear equations using cross multiplication method.
3x − 4y = 2
y − 2x = 7
Solution: The above equation can be rewritten as:
3x − 4y = 2
−2x + y = 7
By method of cross multiplication,
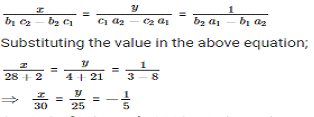
⇒ x = −6 , y = −5
Solving the pair of equations reducible to the pair of linear equations in two variables
- Find the expressions that repeat in both the equations. Give them a simpler form: say x and y.
- Solve the new pair of linear equations for the new variables.
Solve the following system of equations
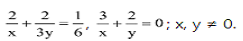
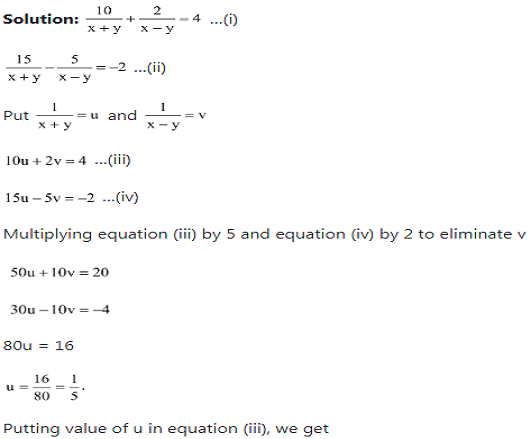
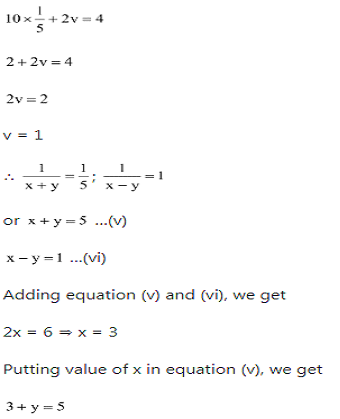
y=2
Therefore, x=3, y=2



