The number system is the most basic chapter of mathematics. It finds its applications in day-to-day life and higher mathematics and physics also. It is imperative to read this chapter carefully to have a robust grip on the successive chapters.
Here get the NCERT Class 9 Maths Chapter 1 notes. It includes the number system explanation, important formula, and pdfs notes.
NCERT Class 9 Maths Chapter 1 Solutions – 2021 Content
Here you get-
- Shor note for Quick Revision
- NCERT Solutions with pdf
- NCERT Exemplar Solutions
- Previous Year Questions bank
- All important Formula Sheets
- Model Answer Sheets designed by practiced teachers.
The study material is updated each year as per the requirements and is consistent with the new syllabus. It is an exclusive feature that the students can enjoy at GharPeShiksha only.
PDF for Class 9 Chapter 1 Number System-
What is a number?
Ann arithmetical value that is used in counting and making calculations. For example- 3,7,0, etc.
Types of numbers
These are the types of numbers-
1. Natural numbers
2. Whole numbers
3. Integers
4. Rational numbers
5. Irrational numbers
6. Real numbers
NATURAL NUMBERS
These numbers are positive numbers that start from ‘1’. It is represented by ‘N’.
For example 1,2,3……so on.
WHOLE NUMBERS
These numbers are the natural numbers including ‘0’. Fractions, negative numbers and decimals are not included. It is represented y ‘W’.
For example 0,1,2,3…….so on.
INTEGERS
These include all whole numbers and negative numbers. Fractions and decimals are not included here. It is represented by ‘Z’.
Integers types- positive, negative and 0.
For example -6,-5, 0,6,12 etc.
RATIONAL NUMBERS
These are the numbers that can be written in the form of p/q where p and q are integers and q is not equal to 0.
For example 3/7, 2/9 -2/5,-10/1 etc.
Note: 0 is also a rational number because it can be written in the form of p/q i.e. 0/1 (0 and 1 are integers)
IRRATIONAL NUMBERS
There are numbers that cannot be written in the
form of p/q where p&q are integer and q is not equal to 0. For example root2
= 1.010024
, pi= 3.14.
REAL NUMBERS
Any number that can be represented on a number line comes under a Real number. It includes both Rational and Irrational numbers.
It is denoted by R.
Important Note:
- All-natural numbers are whole numbers but all whole
numbers need not be natural numbers. - All whole numbers are integers but all integers need not to be whole numbers.
NOTE:
Terminating decimal expansion and Non terminating Recurring decimal expansion are considered
to be Rational numbers because they can be written in the form of p/q.
For example 5.73, 3.898989…..
Non-Terminating non Recurring, decimal expansion is considered to be Irrational number because it cannot be written in the form of p/q.
For
eg 2
2.695124…..
Identities for Irrational numbers
-√ab = √a√b
-(√a+√b) (√a-√b) = a – b
-(a+√b)(a−√b) = a²−b
-(√a+√b)(√c+√d) = √ac+√ad+√bc+√bd
-(√a+√b)(√c−√d) = √ac−√ad+√bc−√bd
-(√a+√b)2 = a+2√(ab)+b
Examples:
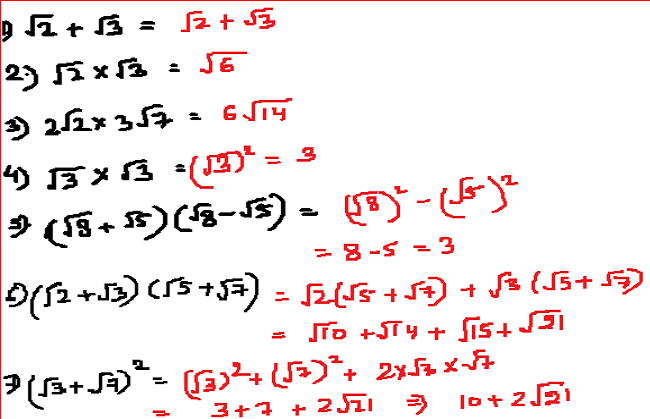
RATIONALISATION
It is the method to convert irrational numbers into rational numbers.

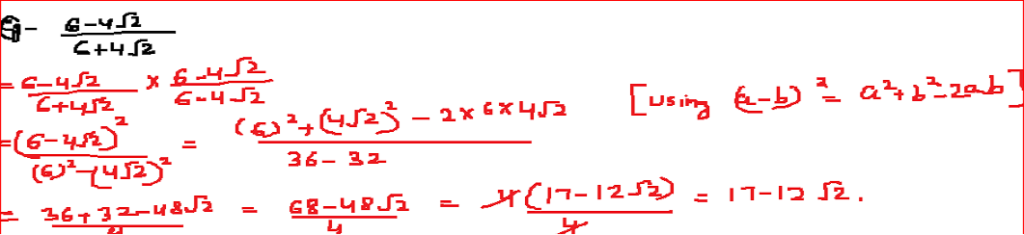
LAWS OF EXPONENTS

For example
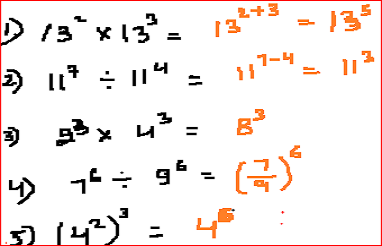
Decimal Expansion of Rational Numbers and Irrational Numbers






