Class 9 Maths Chapter 10 Circles
The circle is a significant chapter of the class 9 maths textbook. It requires a careful and focused reading to get a firm grip on its core concepts. This chapter is also present in the Class 10 mathematics textbook. Therefore it is necessary to read it thoroughly to build a strong base. Circles have been explained outstandingly and in a step-by-step manner in the PDFs provided by GharPeShiksha. The PDFs also contain Revision Notes, NCERT solutions, NCERT Exemplar Solutions, Previous Year Questions of this Chapter, Formulae Sheet, Model Answer Sheets designed by expert teachers. The study material is revised each year as per the syllabus requirements and is consistent with the new exam pattern. It has a lot of practice questions for the students to enhance their understanding. You can avail of it through the website of GharPeShiksha only.
CIRCLE
The set of all the points in a plane that is at a fixed distance from a fixed point makes a circle.
A Fixed point from which the set of points are at fixed distance is called the centre of the circle.
A circle divides the plane into 3 parts: interior (inside the circle), the circle itself and exterior (outside the circle)
Arc– Any smooth curve joining two points is known as Arc. So in Circle, we can have two possible Arcs, the bigger one is known as Major Arc and the smaller one is known as Minor Arc.
Radius
Diameter– Any straight line segment or Chord which passes through the centre of the Circle and its endpoints connects on the boundary of the Circle is known as the Diameter of Circle. So in a circle Diameter is the longest chord possible in a circle.
Chord– Any straight line segment that’s both endpoints falls on the boundary of the circle is known as Chord.
Secant
Tangent
Segment– It is the region between either of its arcs and a chord. It could be a major or minor segment.
Sector
Important theorems
THEOREM 1- Equal chords subtend equal angles at the centre.
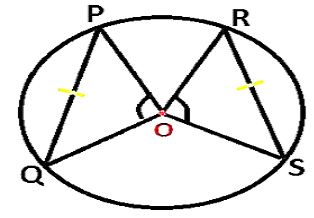
Here in the circle, the two chords are given and PQ = RS with centre O.
So OP = OS = OQ = OR (all are radii of the circle)
∆POQ ≅ ∆SOR
∠POQ = ∠SOR
This shows that the angles subtended by equal chords to the centre are also equal.
Theorem 2– If the angles made by the chords of a circle at the centre are equal, then the chords must be equal (Converse of Theorem 1).
Theorem 3– If we draw a perpendicular from the centre of a circle to any chord then it bisects the chord.
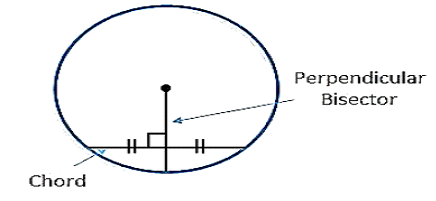
Theorem 4– The line drawn through the centre of a circle to bisects the chord is perpendicular to the chord.
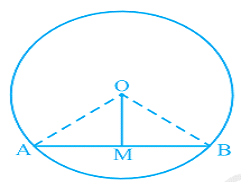
Given: AB is the chord
M is the mid pint of AB.
To prove: OM is perpendicular to AB.
Construction: Join OA & OB
Proof:![]()
OA = OB (Radii)
OM = OM (common)
AM = BM (Given)
Therefore, ΔOMA ≅ ΔOMB (SSS rule)
⇒∠OMA=∠OMB (C.P.C.T)
But, ∠OMA+∠OMB=1800
Hence, ∠OMA=∠OMB=900
⇒OM⊥AB
Theorem 5: Equal chords of a circle are at equal distance(equidistant) from the centre.
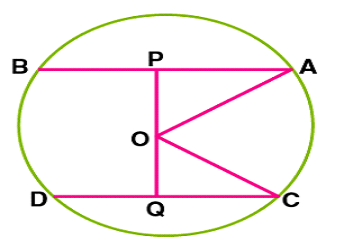
Given– AB = CD, O is the centre.
Join OA and OC.
Construction: Draw OP⊥AB, OQ⊥CD
Proof: In ΔOAP and ΔOCQ,
OA=OC (Radii)
AP=CQ ( AB = CD ⇒(1/2)AB = (1/2)CD (since OP and OQ bisects the chords AB and CD)
ΔOAP ≅ ΔOCQ (RHS rule)
Hence, OP=OQ (C.P.C.T)
Theorem 6: Chords equidistant from the centre of a circle are equal in length.(Converse of Theorem 5)
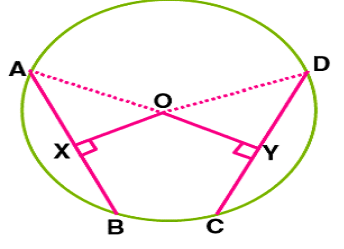
Given OX = OY (The chords AB and CD are at equidistant) OX⊥AB, OY⊥CD
Proof: In ΔAOX and ΔDOY
∠OXA =∠OYD (Both 900)
OA = OD (Radii)
OX = OY (Given)
ΔAOX ≅ ΔDOY (RHS rule)
Therefore AX = DY (CPCT)
Similarly XB = YC
So, AB = CD
Circle through three points
There is one and only one circle passing through three given noncollinear points.
NOTE: A unique circle passes through 3 vertices of a triangle ABC called as the circumcircle .The centre and radius are called the circumcenter and of this triangle, respectively.
ANGLE SUBTENDED BY AN ARC OF A CIRCLE
Theorem 7– The angle subtended by an arc of a circle at the centre is double the angle
subtended by it at any point on the remaining part of the circle.
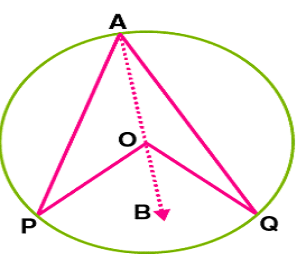
Given: PQ is the arc of a circle with centre O that subtends ∠POQ at the centre.
Cons: Join AO and extend it to B.
Proof: In ΔOAQ OA = OQ….. [Radii]
Hence, ∠OAQ = ∠OQA ……..[Property of isosceles triangle]
∠BOQ = 2∠OAQ …..[Exterior angle of triangle = Sum of 2 interior angles]
Also, ∠BOP = 2∠OAP
⇒∠BOQ + ∠BOP = 2∠OAQ + 2∠OAP
⇒∠POQ = 2∠PAQ
Hence proved.
Angle subtended by diameter on the Circle (Angle in the semi circle)
The angle subtended by diameter on the circle is right angle.
Theorem 8: Angles in the same segment of a circle are equal.
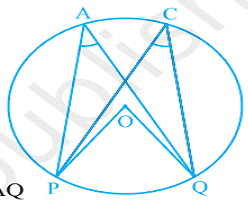
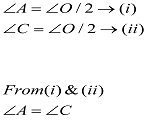
[ Angle subtended by an arc at the centre is double the angle subtendedby it in any part of the circle]
Hence proved.
CYCLIC QUADRILATERAL
Theorem 9: If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, the four points lie on a circle (i.e. they are cyclonic).
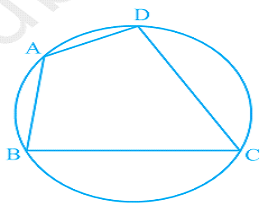
If all the four vertices A, B, C & D lie on the circle then the quadrilateral is known as a Cyclic quadrilateral.
Important:
- The sum of either pair of opposite angles of quadrilateral is 180.
- If the sum of opposite angles of quadrilateral is 180, the it is cyclic.



