What is a triangle?
The plane closed figure, with three sides and three angles is called as a triangle.
Types of Triangles (Based on the sides)
- Equilateral triangle
- Isosceles triangle
- Scalene triangle
Types of Triangles (Based on the sides)
- Acute angled triangle
- Obtuse angled triangle
- Right angled triangle
AREA OF TRIANGLE
Area of triangle or right angle triangle= ½baseheight
Area of equilateral triangle = √3a2/4
Area of isosceles triangle= (1/4) × b × √ (4a2 – b2)
AREA OF TRIANGLE BY HERON’S FORMULA
Area = √[s(s – a)(s – b)(s – c)]
Where s= (a+b+c)/2
Example– A triangle PQR has sides 4 cm, 13 cm and 15 cm. Find the area of the triangle.
Semi perimeter of triangle PQR, s = (4+13+15)/2 = 32/2 = 16 cm
By heron’s formula,
A = √[s(s-a)(s-b)(s-c)]
Hence, A = √[16(16-4)(16-13)(16-15)] = √(16 x 12 x 3 x 1) = √576 = 24 sq.cm
Example–
The sides of triangle are a, a, a units
s=(a+ a+ a)/2=3a/2
Using Heron’s formula
Area of equilateral triangle is
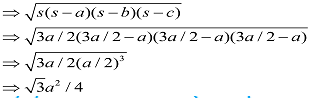
HERON’S FORMULA FOR QUADRILATERAL
Let ABCD he a quadrilateral to find the area of a quadrilateral we need to divide the quadrilateral in triangular parts
Here AB||CD and AC & BD are the diagonals.
AC divides the quad ABCD into two triangles ADC and ABC.
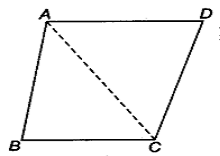
Now we have two triangles here.
Area of quad ABCD = Area of ∆ADC + Area of ∆ABC (Calculate area of triangles by Heron’s formula)



