Class 9 Maths Chapter 13 Surface Area And Volume
Chapter 13 of the Class 9 Mathematics textbook discusses finding the Surface Areas and Volumes of different shapes. A lot of students find it difficult to ace this chapter. This is the most troubling chapter for many students, thanks to the many formulae introduced in this chapter. How should one study this chapter to gain a complete understanding of the concepts? The answer is GharPeShiksha! This chapter has been explained excellently and in a step-by-step manner in the PDFs provided by GharPeShiksha. The PDFs also contain Revision Notes, NCERT solutions, NCERT Exemplar Solutions, Previous Year Questions of this Chapter, Formulae Sheet with memorization techniques, Model Answer Sheets designed by expert teachers. The study material is revised each year as per the syllabus requirements and is consistent with the new exam pattern. It has a lot of practice questions for the students to enhance their understanding. The material is available at the website of GharPeShiksha only.
Plane figure
The figures which we can draw on a piece of paper or which lie on a plane are called Plane Figures.
Example – Circle, Square, Rectangle etc.
Solid figures
The 3D shapes which occupy some space are called Solid Figures.
Example – Cube, Cuboid, Sphere etc.
Volume
Space occupied by any solid shape is the capacity or volume of that figure. The unit of volume is a cubic unit.
Surface Area
The area of all the faces of the solid shape is the total surface area of that figure. The unit of surface area is a square unit.
Lateral or Curved Surface Area
The surface area of the solid shape after leaving the top and bottom face of the figure is called the lateral surface of the shape. The unit of lateral surface area is a square unit.
CUBE
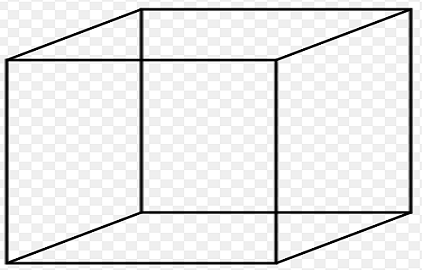
Side= a units
Surface Area
Lateral/Surface area of cube: 4a^2
Total surface area of cube: 6a^2
Example: What is the surface area of a cube of side 5 cm?
Solution:
Given,
Side of the cube = a = 5 cm
Surface Area of a Cube = 6a2
= 6 × 52 cm2
= 6 × 25 cm2
= 150 cm2
Volume
Volume of cube: a^3
CUBOID
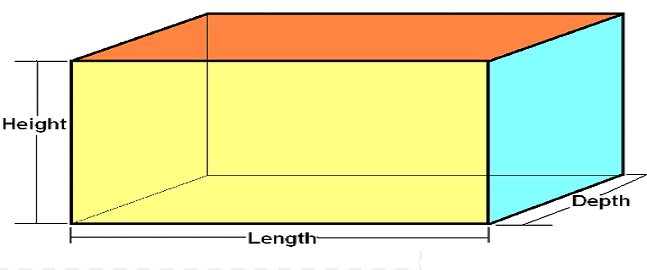
Here, l= length
b= breadth/width
h= height/depth
Surface Area
Lateral/Surface area of cuboid: 2 (l+b)h
Total surface area of cuboid: 2 (lb+bh+hl)
Volume
Volume of cuboid: lbh
Example: The dimensions of a cuboid are given as follows:
Length = 4.8 cm
Width = 3.4 cm
Height = 7.2 cm.
Find the Total Surface area and the Lateral Surface area.
Solution:
The total surface area is given as
TSA = 2 (lb + bh + hl)
=2((4.8 ×3.4) + (3.4×7.2) + (7.2×4.8))
= 2(16.32 +24.48 +34.56)
= 2(75.36) cm²
Therefore, TSA of a cuboid= 150.72![]()
Also, the lateral surface area = 2 h (l + b)
= 2×7.2 (4.8 + 3.4)
= 14.4 (8.2) = 118.08
Therefore, LSA of a cuboid = 118.08 cm²
CONE
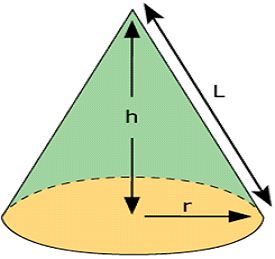
Here, r= radius
h= height
l= slant height
Surface Area
Lateral/Curved Surface area of cone:![]()
Total surface area of cone:![]()
NOTE: To calculate its slant height ![]()
Volume
Volume of cone:![]()
Example: Calculate the Total surface area of a cone whose radius is 8 cm and height is 12 cm.
Solution– We know that the total surface area is given as
πr (r+l)
Also, l=![]()
Also, l= ![]() =
= ![]() =14.42cm
=14.42cm
Thus Total Surface Area = π(8)(8+14.42)
= π(8)(22.42)
=179.36π
CYLINDER
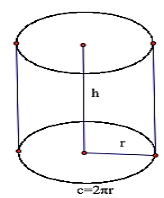
Here, r= radius
h= height
Surface Area
Lateral/Curved Surface area of cylinder:![]()
Total surface area of cylinder:![]()
Volume
Volume of cylinder:![]()
Example: What will be the surface of the cylinder with height 10 cm and the diameter of the base is 12 cm.
Solution:
h = 10 cm, d = 12 cm
Hence, R = d/2 = 12/2 = 6 cm
According to the formula:
TSA = 2πr(r+h)
=2×3.14×6(6+10)
=602.88cm2
HOLLOW RIGHT CIRCULAR CYLNDER
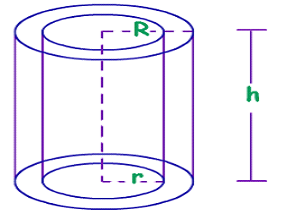
Surface Area
Lateral/Curved Surface area of cylinder:![]()
Total surface area of cylinder:![]()
Volume
Volume of cylinder:![]()
Example: Find the curved surface area of a hollow cylinder with thickness 2 cm external radius 8 cm and height is 20 cm.
Solution: Let the external radius, the internal radius and the height of the hollow cylinder be r1, r2 and h respectively.
r2= 8-2 = 6 cm.
Curved surface area of a hollow cylinder = 2πh(r1+r2)=2×227×20(8+6)=1760cm2
SPHERE
Here, r= radius
Surface Area
Lateral/Curved Surface area of sphere:![]()
Total surface area of sphere:![]()
Volume
Volume of sphere:![]()
EXAMPLE: If the radius of a sphere is 3r then what is its volume?
Solution: Volume of sphere:![]()
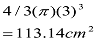
HEMISPHERE
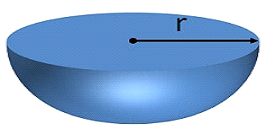
Here r= radius
Lateral/Curved Surface area of hemisphere:![]()
Total surface area of hemisphere:![]()
Volume
Volume of hemisphere:![]()
Example: Find the total surface area of a hemisphere and a solid hemisphere each of radius 10 cm. (π=3.14)
Solution:
Radius of a hemisphere = Radius of a solid hemisphere = 10 cm (Given)
Surface area of the hemisphere = 2πr2
= 2×3.14×(10)2 cm2
= 628 cm2
And, surface area of solid hemisphere = 3πr2
= 3×3.14×(10)2 cm2
= 942 cm2



