CBSE Class 9 Maths Chapter 15 Solutions – Download Free PDF Notes
Probability is a new chapter introduced in the Class 9 mathematics textbook. It is an easy chapter as per Class 9 but has roots in the higher classes. Thus, it is imperative to study the chapter thoroughly to have a complete understanding of its concepts. Students can study this chapter from the notes provided by GharPeShiksha. The study material contains Revision Notes, NCERT solutions, NCERT Exemplar Solutions, Previous Year Questions of this Chapter, Formulae Sheet, Model Answer Sheets designed by expert teachers. The study material is revised each year as per the syllabus requirements and is consistent with the new exam pattern. It has a lot of practice questions for the students to enhance their understanding. You can avail the notes using the website of GharPeShiksha only.
Introduction of Probability
- Probability is the measure of the likelihood of an event to occur. Events can’t be predicted with certainty but can be expressed as to how likely it can occur using the idea of probability.
- Probability can range between 0 and 1, where 0 probability means the event to be an impossible one and probability of 1 indicates a certain event.
Terms to Remember:
Experiment- It is any procedure that can be infinitely repeated or any series of actions that have a well-defined set of possible outcomes.
Event– An event is an outcome or defined collection of outcomes of a random experiment.
Favourable Events– The outcomes which make necessary the happening of an event in a trial are called favourable events.
Unfavourable Events– The outcomes which do not make necessary the happening of an event in a trial are called favourable events.
Sure Event– An event which always occurs whenever the random experiment is performed.
Impossible Event- An event which never occurs whenever the random experiment is performed.
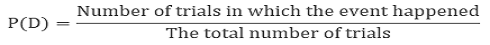
Important Events
- COIN TOSSING
When we flip a coin there is always a probability to get a head or a tail is 50 percent.
Suppose a coin tossed then we get two possible outcomes either a ‘head’ (H) or a ‘tail’ (T), and it is impossible to predict whether the result of a toss will be a ‘head’ or ‘tail’.
Total number of possible outcomes = 2
(i) If the favorable outcome is head (H).
Number of favorable outcomes = 1.
Therefore, P (getting a head)
= P(H) = Number of favourable outcomes/ total number of possible outcomes
= 1/2.
(ii) If the favourable outcome is tail (T).
Number of favourable outcomes = 1.
Therefore, P(getting a tail)
Number of favourable outcomes
= P(T) = total number of possible outcomes
= 1/2.
- ROLLING OF DICE
When a fair dice is rolled once, the number that comes up top is either 1, 2, 3, 4, 5 or 6.
Assuming we roll the dice once, to check the possibility of ‘3’ coming up.
Number of possible outcomes = 6
Number of outcomes to get ‘3’ = 1
The probability of getting ‘3’ =Number of outcomes to get 3/Number of possible outcomes
=1/6
When two dice are rolled, Let (a,b) denote a possible outcome of rolling the two die, with a the number on the top of the first die and b the number on the top of the second die.
SAMPLE SPACE
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
the outcomes where the sum of the two dice is equal to 5 form an event. If we call this event E, we have
E={(1,4),(2,3),(3,2),(4,1)}.
P(E)= 4/36=1/9
- DRAWING A CARD
The number of cards in a pack of playing cards is 52. It consists of 4 suits of 13 cards. They are spades, hearts, clubs, and diamonds. Spades and clubs are black while hearts and diamonds are red. Each suit contains an ace, king, queen, jack or knaves, 10, 9, 8, 7, 6, 5, 4, 3, and 2. King, Queen, and Jack (or Knaves) are called the face cards. In the deck of 52 playing cards, there are 12 face cards.

Problems on cards
Things to Remember
All favourable and unfavourable event outcomes come from the well-defined set of outcomes.
The probability of favourable and unfavourable events happening depends upon the number of trials performed. However, the sum of both these probabilities is always equal to one.
Example: There are 6 fruits in a bowl, 3 are apple, 2 are guava and 1 is banana. What is the probability of picking a guava?
The probability is the number of guava in the bag divided by the total number of fruits = P(A) = No. of favorable outcomes / Total number of possible outcomes
= P(A) = 2 / 6 = 1 / 3.
Example: Compute the probability of the occurrence of an event if the probability the event not occurring is 0.56.
Solution:
Given,
P (not E) = 0.56
We know that,
P (E) + P (not E) = 1
So, P (E) = 1 – P (not E)
P (E) = 1 – 0.56
Or, P (E) = 0.44



