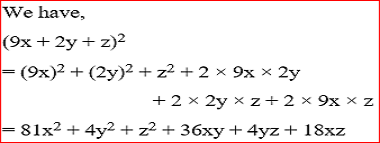CBSE Notes for Class 9 Maths Chapter 2 – Polynomials

CBSE Class 9 Maths Chapter 2 Polynomials Solutions

What is a Polynomial?
These are the algebraic expressions that consists of variables and coefficients. The word is derived from two Greek words ‘poly’ means many and ‘nominal’ means terms.

Therefore polynomial can have many terms.

NOTE– We can perform arithmetic operations such as addition, subtraction, multiplication but not division by variable.
Let us study about Degree, Terms, Types of polynomial, Solving
the polynomial and Arithmetic Operations.

DEGREE OF A POLYNOMIAL
It is defined as the highest power within a polynomial. So, the largest exponent of a variable is called the degree of a polynomial.

TERMS OF A POLYNOMIAL
These are the parts of the equation which are generally separated by positive or negative signs. Each part is considered to be a term in that equation.

DECIMAL REPRESENTATION OF RATIONAL NUMBERS:

TYPES OF POLYNOMIAL
The Polynomials are classified into 3 types based on the number of terms and degree.
POLYNOMIAL on the basis of number of terms-
1.Monomial
2.Binomial
3 Trinomial.
POLYNOMIAL on the basis of degree-
1 Constant or Zero Polynomial.

Linear Polynomial

Quadratic polynomial

Cubic Polynomial.
5.Biquartic Polynomial
CONSTANT– A constant term is a term in an algebraic expression that has a value that is constant or cannot change. For example 3 is a constant.
VARIABLE -A variable is a quantity that may change within the context of a mathematical problem or experiment. Typically, we use a single letter to represent a variable. The letters x, y, and z are common generic symbols used for variables.
EXPONENT– An exponent refers to the number of times a number is multiplied by itself. For example 2^3= 222=8
ZERO OF A POLYNOMIAL
Zeros of a polynomial can be defined as the points where the polynomial becomes zero as a whole. A polynomial having value zero (0) is called zero polynomial. Sometimes, they are also referred to as roots of the polynomials.

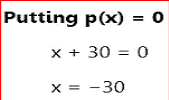
STANDARD FORM OF A POLYNOMIAL
It is the form of polynomial where the highest degree is the first term followed by other terms.
For example- 3x^4 + x^3 – 2x^2 + 7x (first the highest degree, the lower one and then constant).

REMAINDER THEOREM
Let p(x) be any polynomial of degree greater than or equal to one and ‘a’ be any real number. If p(x) is divided by the linear polynomial x – a, then the remainder is p (a). This is the remainder theorem.
That is when we divide p(x) by x-a we obtain
p(x) = (x-a)·q(x) + r(x),
as we know that Dividend = (Divisor × Quotient) + Remainder
Example: Find the remainder whent3–2t2+t+1 is divided by t – 1.
Solution: Here, p(t)=t3–2t2+t+1, and the zero of t – 1 is 1.
∴ p (1) = (1)3 – 2(1)2 + 1 + 1= 2

By the Remainder Theorem, 2 is the remainder when t3–2t2+t+1 is divided by t – 1.

FACTOR THEOREM
Factor theorem is commonly used for factoring a polynomial and finding the roots of the polynomial. It is a special case of a polynomial remainder theorem.
According to factor theorem, if f(x) is a polynomial of degree n ≥ 1 and ‘a’ is any real number, then, (x-a) is a factor of f(x), if f(a)=0.
Also, we can say, if (x-a) is a factor of polynomial f(x), then f(a) = 0.

Consider the polynomial function f(x)= x2 +2x -15
Solving the equation, assume f(x)=0, we get:
x2 +2x -15 =0
x2 +5x – 3x -15 =0
(x+5)(x-3)=0
(x+5)=0 or (x-3)=0
x = -5 or x = 3
Therefore, (x+5) and (x-3) are factors of x2 +2x -15
Also, -5 and 3 are the solutions to the equation x2 +2x -15=0
Verify-
If x = -5 is the solution, then
f(x)= x2 +2x -15
f(-5) = (-5)2 + 2(-5) – 15
f(-5) = 25-10-15
f(-5)=25-25
f(-5)=0
If x=3 is the solution, then;
f(x)= x2 +2x -15
f(3)= 32 +2(3) – 15
f(3) = 9 +6 -15
f(3) = 15-15
f(3)= 0

Algebraic Identities 
(x + y)2 = x2 + 2xy + y2
(x – y)2 = x2 – 2xy + y2
x2 – y2 = (x + y) (x – y)
(x + a) (x + b) = x2 + (a + b)x + ab.
(x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2zx.
(x + y)3 = x3 + y3 + 3xy(x + y)
(x – y)3 = x3 – y3 – 3xy(x – y)
x3 + y3 + z3 – 3xyz = (x + y + z) (x2 + y2 + z2 – xy – yz – zx)

1.Solve (x + 3) (x – 3) using algebraic identities.
x2 – 32 = x2 – 9.

2.Solve (x + 5)3 using algebraic identities.
(x + 5)3 = x3 + 53 + 3.x.5(x+5)
= x3 + 125 + 15x(x+5)
= x3 + 125 + 15×2 + 75
= x3 + 15×2 + 200 

3.(x + 1)(x + 1)
(x + 1)2 = (x)2 + 2(x)(1) + (1)2 = x2 + 2x + 1

4.Factorise 16×2 + 4y2 + 9z2 – 16xy + 12yz – 24zx
16×2 + 4y2 + 9z2 – 16xy + 12yz – 24zx = (4x)2 + (-2y)2 + (-3z)2 + 2(4x)(-2y) + 2(-2y)(-3z) + 2(-3z)(4x)= (4x – 2y – 3z)2 = (4x – 2y – 3z)(4x – 2y – 3z)

5.Expand (3x – 4y)3
(3x – 4y)3 = (3x)3 – (4y)3– 3(3x)(4y)(3x – 4y) = 27×3 – 64y3 – 108x2y + 144xy2

 6.Factorize (x3 + 8y3 + 27z3 – 18xyz)
(x3 + 8y3 + 27z3 – 18xyz) = (x)3 + (2y)3 + (3z)3 – 3(x)(2y)(3z)= (x + 2y + 3z)(x2 + 4y2 + 9z2 – 2xy – 6yz – 3zx)
Write the following in expanded form :
(i) (9x + 2y + z)2