Class 9 Maths Chapter 4 Linear Equations In Two Variables
DEFINITION:
When an equation has two variables both of degree one, then that equation is known as linear equation in two variables.
Standard form= ax+by+c=0. (where a, b & c are constants and a,b are not equal to 0.
NOTE: The solution can be found by assuming the value of one of the variable and then proceed to find the other solution.
There are infinitely many solutions for a single linear equation in two variables.
The pair which satisfies the equation is the solution of that particular equation.
Slope Intercept form
Generally, the linear equation in two variables is written in the slope-intercept form as this is the easiest way to find the slope of the straight line while drawing the graph of it.
The slope-intercept form is
y=mx + c
Here, m represents the slope of the line.
To find the solution of a Linear Equation
1.There is only one solution in the linear equation in one variable but there are infinitely many solutions in the linear equation in two variables.
2.As there are two variables, the solution will be in the form of an ordered pair, i.e. (x, y).
3.The pair which satisfies the equation is the solution of that particular equation.

GRAPHICAL REPRESENTATION OF THE LINEAR EQUATION
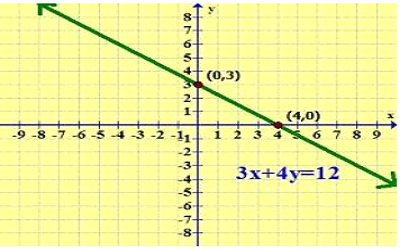
For example, Draw the graph of the equation 3x + 4y = 12.
We need to find the solutions of the equation first-
Let x = 0
3(0) + 4y = 12
y = 3
Let y = 0
3x + 4(0) = 12
x = 4
Now draw a table to write the solutions.
| x | 0 | 4 |
| y | 3 | 0 |
Now we can draw the graph easily by plotting these points on the Cartesian plane.

NOTE:
Lines passing through the origin
1. Certain linear equations exist such that their solution is (0, 0). Such equations when represented graphically pass through the origin.
2.The coordinate axes namely x-axis and y-axis can be represented as y=0 and x=0, respectively.
3.Equations of the form y=mx passes through the origin.2
Lines parallel to coordinate axes
1.Linear equations of the form y=a, when represented graphically are lines parallel to the x-axis and a is the y-coordinate of the points in that line.
Example- y=3
Linear equations of the form x=a, when represented graphically are lines parallel to the y-axis and a is the x-coordinate of the points in that line.
X= 4
How to represent linear equation of one variable in two variables?
Example x=3 (in one variable)
Sol: 1.x + 0.y=3 (in two variable)
2y=5 (in one variable)
0.x + 2.y=5 (in two variable)



