Class 9 Maths Chapter 8 Quadrilaterals
A Quadrilateral is a shape made by four sides arranged in a specific manner. Rectangle, Square, Rhombus, etc., are examples of Quadrilaterals that you will study in this chapter. This chapter is pretty simple, and it has the potential to fetch good marks for you in the exam, provided you study it from a good source. You can read it from the particular module provided at GharPeShiksha. It contains all the crucial points along with a step-by-step explanation. It also includes Revision Notes, NCERT solutions, NCERT Exemplar Solutions, Previous Year Questions of this Chapter, Formulae Sheet, Model Answer Sheets designed by expert teachers. The study material is updated each year as per the syllabus requirements and is consistent with the new exam pattern. It has a lot of practice questions for the students.
QUADRILATERAL
It is a plane figure bounded by four sides and four vertices. The total sum of all the four angles of a quadrilateral is 360.
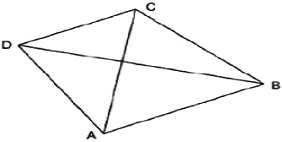
Here, AB,BC,CD & DA are the sides.
A,B,C,D are the vertices of quadrilateral ABCD.
Line segments AC & BD are the diagonals.
Special types of Quadrilateral
- Parallelogram
- Rectangle
- Square
- Rhombus
- Trapezium
Properties of Quadrilateral
- Every quadrilateral has four sides and four vertices.
- The sum of its interior angles is 360.
PARALLELOGRAM
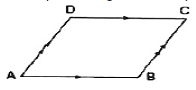
Here, AB || CD and AD || BC.
- Opposite sides of a parallelogram are equal.
- Opposite sides of a parallelogram are equal.
- AC & BD are the diagonals.
- The diagonal divides it into two congruent triangles.
Area of parallelogram= Base * Height
RECTANGLE
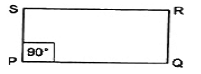
- Opposite sides are equal and parallel.
- Each angle is 90.
- Diagonals are equal and bisect each other.
Area of Rectangle= Length * Breadth
SQUARE
- All four sides are equal.
- Each angle is 90.
- Both diagonals are equal.
- Diagonals bisect each other at 90.
Area of Square= Side * Side
RHOMBUS
- All four sides are equal.
- Diagonals are not equal.
- Each angle is 90.
- Diagonals do not bisect each other at 90.
Area of rhombus = ½ * Product of two diagonals
= ½ * d1 * d2
TRAPEZIUM
- One pair of opposite sides are parallel.
- One pair of opposite sides are non parallel.
- Diagonals bisect each other.
- Sum of adjacent angles is 180.
Area of Trapezium = ½ * (sum of two parallel sides) * distance between them
NOTE: If two non parallel sides are equal, then it is called an Isosceles trapezium.
KITE
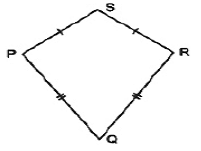
Here, PQ=QR & PS=SR
- Two pairs of adjacent sides are equal.
- Diagonals intersect each other at right angles.
- Longer diagonal bisects the other diagonal.
IMPORTANT POINTS TO BE REMEMBER:-
- A square is a rhombus but a rhombus is not a square.
- A square is a rectangle but a rectangle is not a square.
- A square, rectangle and rhombus are all parallelogram.
- A parallelogram is a trapezium but a trapezium is not a parallelogram.
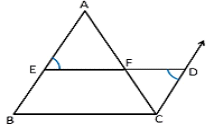
The Mid-Point Theorem
The line segment joining the midpoints of two sides of a triangle is parallel to the third side and is half of the third side.
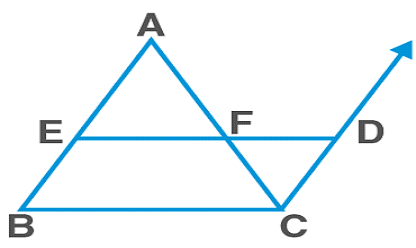
In ΔABC, E – the midpoint of AB; F – the midpoint of AC
Construction: Produce EF to D such that EF=DF.
In ΔAEF and ΔCDF,
AF=CF [ F is the midpoint of AC]
∠AFE=∠CFD [ V.O.A]
EF=DF [ Construction]
∴ΔAEF≅ΔCDF [SAS rule]
Hence,
∠EAF=∠DCF…(1)
DC=EA=EB [ E is the midpoint of AB]
DC‖EA‖AB [Since, (1), alternate interior angles]
DC‖EB
So EBCD is a parallelogram
Therefore, BC=ED and BC‖ED
Since, ED=EF+FD=2EF=BC [ ∵ EF=FD]
We have,EF=12BC and EF||BC
Hence proved
Converse of Mid Point Theorem
The line drawn through the mid-point of one side of a triangle, parallel to another side, intersects the third side at its mid-point.